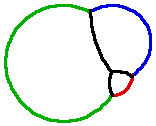
Soap films and soap bubbles are examples of “minimal surfaces,” so-called because nature selects the shape that requires the least amount of total energy to maintain, and thus enclose a given area/volume with as little perimeter/surface area as possible. (A circle takes the least perimeter to surround a given amount of area; and a sphere is the shape of least surface area that encloses a given amount of volume.)
The general problem of determining the shape of the minimal surface constrained by a given boundary is known as Plateau’s Problem, named after Joseph Antoine Ferdinand Plateau, a nineteenth-century, blind, Belgian physicist, who “observed” a handful of simple patterns that seemed to completely describe the geometry of how soap bubbles fit together. Plateau claimed that soap bubble surfaces always make contact in one of two ways: either three surfaces meet at 120-degree angles along a curve; or six surfaces meet at a vertex, forming angles of about 109 degrees.
For instance, in a cluster of bubbles, two bubbles (of possibly different sizes) that intersect will have a common “dividing wall” (the third surface), which meets the outer surfaces of the bubbles in 120-degree angles. And the edges of the six soap-film faces that emerge within a tetrahedral wire frame, when dipped in a soapy solution, form angles of roughly 109 degrees at a “central vertex.”
Until Jean Taylor came along in the mid-1970’s, Plateau’s patterns were just a set of empirical rules. As a follow-up to her doctoral thesis, she was able to prove that Plateau’s rules were a necessary consequence of the energy-minimizing principle — no other yet unobserved configurations were possible — thus settling a question that had been open for more than a hundred years.
The forces acting along the surface of a soap bubble all have the same magnitude in all directions. In crystals this is not the case (magnitudes of surface forces differ in different directions, though they may exhibit a “grain,” analogous to that in a piece of wood), but they still require the least energy to enclose a given volume. Minimal surfaces that model these conditions, like a cube with its corners chopped off or the bottom half of a cone mounted on a cylinder, are known as Wulff Shapes, and provide fertile ground for mathematical mining today.
Wulff shape for beryllium aluminum silicate
Last Updated February 7, 2022